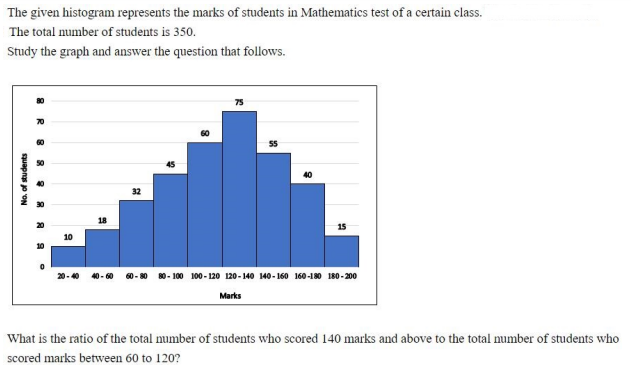
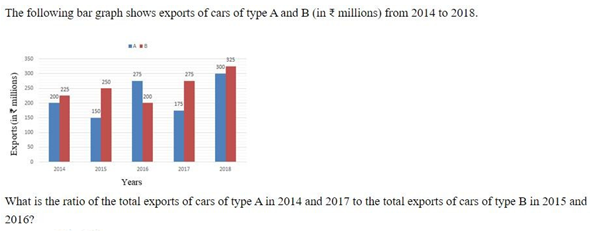
Question
The ratio of age of A and B after 8 years is 4:5
respectively. The ratio of age of A and C 6 years ago is 3:4 respectively. If the present average age of A and C is 30 years, then find the present age of C.Solution
ATQ,
The ratio of A and B's ages after 8 years is 4:5, so we get the equation 5(A+8)=4(B+8), which simplifies to 5A−4B=−8. The ratio of A and C's ages 6 years ago is 3:4, giving us the equation 4(A−6)=3(C−6), which simplifies to 4A−3C=6. The average age of A and C is 30, so A+C=60. Solving the system of equations, we substitute A = 60 − C into the second equation and solve to get C=33.43. Thus, the present age of C is approximately 33.43 years.
Which of the following Schemes/initiatives have played major role in the inclusion of the disadvantaged groups under the formal economic net.
...
Which of the following is a discount instrument in the Indian money market?
Which city reclaimed the third position in the GFCI 36 ranking from Singapore?
As per the proposed changed in the ECB Framework, the outstanding ECB limit is to be _______
The India-UK Infrastructure Financing Bridge (UKIIFB) aims to boost collaboration in what sector?
Who has the power to give directions under IFSCA Act?
In the IFSCA Listing Regulations 2024, what is the maximum period for which the price stabilization process under the Green Shoe Option can be active po...
Consider the following about the Vision of Amrit Kaal:
I.             Opportunities for Citizens with a focus on the Youth.
...According to the IFSCA Circular on facilitating investments by NRIs and OCIs (May 2024), what is the minimum number of investors required for a retail s...
Under the IFSCA (BATF) Regulations 2024, how long does the Authority have to process an application for relaxation of strict regulatory enforcement?
Relevant for Exams:
