Question
Given below is a question followed by two statements
numbered I and II, each containing some information. Decide which of the statement(s) is/are sufficient to answer the question. The sum of ages of A, B and C is 65 years. What is B's age? Statements: I. B is 15 years younger than A. II. C is 40 years old.Solution
Statement: I. B is 15 years younger than A. This statement alone is not sufficient to determine B's age because it provides a relationship between the ages of A and B, but we need the actual age of A or B to find B's age. II. C is 40 years old. This statement alone is not sufficient either because knowing C's age does not provide any information about B's age or the relationship between A and B. Now, let's combine the statements: If we know that C is 40 years old (Statement II) and we also know the relationship between the ages of A and B (Statement I), we can find B's age. However, if we only know Statement I or Statement II alone, it is not sufficient to determine B's age. Therefore, the answer is both statements together (I and II) are required to answer the question.
(1748 ÷ 8) + 76.8 × 35 =(? × 4) + (42 × 35.5)
(560 ÷ 32) × (720 ÷ 48) = ?
What will come in the place of question mark (?) in the given expression?
642 - 362 = ? X √1225
- Calculate the value of x if x% of 400 plus {800 ÷ x of 8} × 4 is equal to 88
Simplify the following expression:
(3/5 of 250 + 40% of 150) ÷ (0.75 of 80)
Train M, ‘x’ metres long crosses (x – 30) metres long platform in 22 seconds while train N having the length (x + 30) metres crosses the same plat...
(92.03 + 117.98) ÷ 14.211 = 89.9 – 30.23% of ?
- What will come in place of (?), in the given expression.
(81 ÷ 9) + (121 ÷ 11) + (64 ÷ 8) = ? 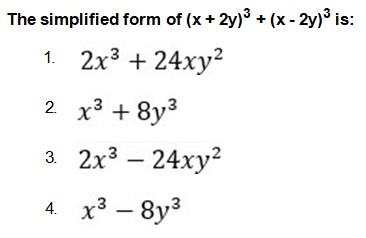
Find the simplified value of the given expression:
7 of 9 ÷ 3 × 5² + √81 – 14



