📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!

    Question

    Seven persons namely – Reena, Heena, Gautam, Ziyana,

    Hari, Rohit and Jyoti are sitting in a row not necessary in same order in such a way that some are facing north while others are facing south. Reena sits third to left of Hari, either of them sits at end of the row and Rohit sits immediate left of Reena. Rohit sits second to left of Ziyana, who is facing south. How many person sits facing south? I. Person sitting immediate neighbor of Ziyana sits fourth to right of Jyoti. Person sitting at end of the row sits facing in opposite direction and Gautam sits third from right end. Hari faces north direction. II. Person sitting immediate left of Rohit sits fourth to right of Jyoti and Gautam sits second to left of Hari. Each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question:
    A If the data in Statement I alone is sufficient to answer the question, while the data in Statement II alone is not sufficient to answer the question. Correct Answer Incorrect Answer
    B If the data in Statement II alone is sufficient to answer the question, while the data in Statement I alone is not sufficient to answer the question. Correct Answer Incorrect Answer
    C If the data either in Statement I alone or in Statement II alone is sufficient to answer the question. Correct Answer Incorrect Answer
    D If the data in both the Statements I and II together are not sufficient to answer the question. Correct Answer Incorrect Answer
    E If the data in both the Statements I and II together are necessary to answer the question. Correct Answer Incorrect Answer

    Solution

    We have:   Reena sits third to left of Hari, either of them sits at end of the row, which means we get two possibilities, in case (1) Hari sits facing north at right end and in case (2) Reena sits at extreme left end.   Rohit sits immediate left of Reena and Rohit sits second to left of Ziyana, who sits facing south, that means case (2) is not valid, in case (1a) Reena sits facing south and in case (1b) Reena sits facing north. Based on above given information we get: 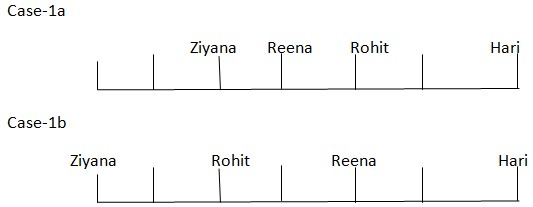From I: We have: Person sitting immediate neighbor of Ziyana sits fourth to right of Jyoti, which means Jyoti must sits facing south.  Person sitting at end of the row sits facing in opposite direction, which means person at left end sits facing south. Gautam sits third from right end, which means case (1a) is not valid. Based on above given information, we have following result: 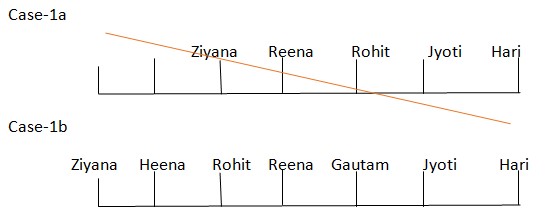Case1a Gautam sits third from right end, this condition is not satisfied so rejected. Since, direction facing of Heena, Rohit and Gautam is not known, thus we can’t determine required result. Hence, statement I is not sufficient. From II: We have:  Person sitting immediate left of Rohit sits fourth to right of Jyoti, which means in case (1a) Rohit sits facing south and in case (1b) Rohit sits facing north. Gautam sits second to left of Hari, which means case (1a) is not valid. Based on above given information, we get following result: case-1b Since, direction of Heena and gautam is not known, thus result can’t be determined. Hence, statement II is not sufficient. From I and II: Based on above given statements we get: Case-1b Since, direction of Heena and Gautam is not known, thus result can’t be determined. Hence, statement I and II together are not sufficient.

    Practice Next
    More Data Sufficiency Questions

    Relevant for Exams:

    ask-question