New Enroll in RBI Grade B New Batch - Starts on May 21

    Question

    A square and a regular hexagon are drawn such that all

    the vertices of the square and the hexagon are on circle of radius r cm. The ratio of area of the square and the hexagon is
    A 3 : 4 Correct Answer Incorrect Answer
    B 4 : 3√3 Correct Answer Incorrect Answer
    C √2 : √3 Correct Answer Incorrect Answer
    D 1 : √2 Correct Answer Incorrect Answer

    Solution

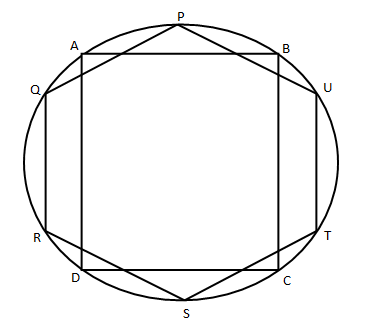    Here ABCD is a square and PQRSTU is Hexagon Let o is the center of circle then diagonal of square ABCD will 2r then area of square will be ½ (d)2 => ½ (2r)2 => 2r2 Now we have to find the area of hexagon we know that O angle is 60° then and ∠ S = ∠ T, then ∆ OST will be equilateral ∆, having side r. ∆OST = √3/4 × r2 In the Hexagon there will be 6 triangle and all are same then area of Hexagon will be => 6 × √3/4 × r2 (3√3/2) × r2 Ratio => Square : Hexagon => (2r/2) : (3√3/2) × r2 => 4 : 3√3

    Practice Next