📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!

    Question

    In the question, two quantities I and II are given. You

    have to solve both the quantities to establish the correct relation between Quantity-I and Quantity-II and choose the correct option. Quantity I: A 200 litres chemical mixture contains 25% acid and the rest is water. How much water should be added so that the final acid to water ratio becomes 1:3? Quantity II: In a container, the ratio of honey to water is 7:2. If 21 litres of honey and 24 litres of water are added, the ratio becomes 2:1. Find the initial difference in litres between honey and water.
    A Quantity-I > Quantity-II Correct Answer Incorrect Answer
    B Quantity-I < Quantity-II Correct Answer Incorrect Answer
    C Quantity-I ≤ Quantity-II Correct Answer Incorrect Answer
    D Quantity-I ≥ Quantity-II Correct Answer Incorrect Answer
    E Quantity-I = Quantity-II or No relation Correct Answer Incorrect Answer

    Solution

    ATQ,

    Quantity I:

    Acid = 25% of 200 = 50 litres

    Water = 75% of 200 = 150 litres

    Let added water = x litres 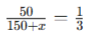Image

    50×3=1×(150+x)

    150=150+x

    X = 0

    Water to be added = 0 litres

    Quantity II:

    Let honey = 7x, water = 2x

    New honey = 7x + 21, new water = 2x + 24

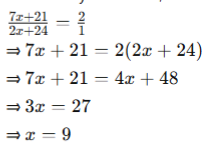
    Image

    Initial difference = 7x – 2x = 5x = 5 × 9 = 45 litres

    So, Quantity-I < Quantity-II

    Practice Next
    More Quantity Inequality Questions

    Relevant for Exams:

    ask-question