Question
Two circles of radius 13 cm and 15 cm intersect each
other at points A and B. If the length of the common chord is 12 cm, then what is the distance between their centres?Solution
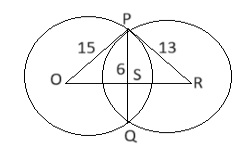Let O and R be the center of the circle and PQ be the length of the common chord. OP = 15, RP = 13 PS = 1/2 PQ (as perpendicular from the center of the circle to a chord bisects the chord) PS = 1/2 × 12 PS = 6 By applying Pythagoras theorem in PSO: OS2 = OP2-PS2 = 152 – 62 = 225-36 = 189 OS = √189 By applying Pythagoras' theorem in PSO': RS² = RP2-PS2 = 132 - 62 = 169-36 = 133 RS = √133 OR = OS + RS = √189 + √133 The distance between their centers = √189 + √133
Doubt pour over (A)/ me like hot fudge on (B)/ salted caramel ice cream. (C) / No error (D)
- Read each sentence to find out whether there is any grammatical error in it. The error, if any, will be in one part of the sentence. Mark the part with the...
this week since February 2018 / companies adding 18 oil rigs this week / U.S. energy firms added the most oil rigs / producers have been reducing spendi...
In the following question, some part of the sentence may have errors. Find out which part of the sentence has an error and select the appropriate optio...
Have we made headway in our attempts to save the world’s rain forests?
I was surprised (A) / when the hostess smiled (B) / as if she saw me before (C) / No Error (D)
Recently a number of (1)/ policemen was sentenced (2)/ to death for their complicity (3)/ in the murder (4)/ No error (5)
In the following questions, one part of the sentence may have an error. Find out which part of the sentence has an error and select the appropriate opti...
I have been knowing(1)/ him for the last(2)/ five years but now I don’t(3)/ know where he lives.(4)
Despite its widespread popularity (A)/among Florida's politicians, (B)/the bond cap statue was not (C)/entirely kosher from a constitutional point of vi...
Relevant for Exams:
