Question
Find the least 4-digit number which, when divided by
21, 28, and 12, leaves a remainder of 3 in each case.Solution
Prime factorization of 21 = 3 × 7
Prime factorization of 28 = 2² × 7
Prime factorization of 12 = 2² × 3 LCM of (21, 28, and 12) = 2² × 3 × 7 = 84 Least 4-digit number divisible by 84 = 1,008 So, required number = 1008 + 3 = 1,011 Hence, option A.
- Simplify the following trigonometric expression:
15 cos 27° sec 63° − 9 cot 61° tan 29° If √3 tan 2θ – 3 = 0, then find the value of tanθ secθ – cosθ where 0 < θ < 90°
If (cos A - sin A) = √2 cos (90° - A), then find the value of cot A.

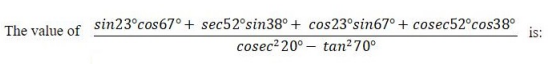
If tan 3.5θ x tan 6.5θ = 1 then the value of tan 5θ is
Find the maximum value of 14 sin A + 24 cos A.
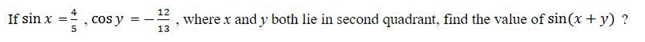
- If cos θ = (4x² – 1)/(1 + 4x²) then find the value of sin q.
The minimum value of 9 cos2 θ + 36 sec2 θ is


