Question
How many numbers between 200 and 1000 are divisible by both
20 and 30?Solution
ATQ,
A number divisible by both 20 and 30 must be divisible by L.C.M. of 20 and 30 = 60
We look for numbers divisible by 60 in the given range:
First term (a) = 60 × 4 = 240
Common difference (d) = 60
Last term (L) = 60 × 16 = 960
Let the number of terms be n.
Use the A.P. formula:
a + (n - 1)d = L
Substitute values:
240 + (n - 1) × 60 = 960
⇒ 240 + 60n - 60 = 960
⇒ 60n = 780
⇒ n = 780 ÷ 60 = 13
7(1/7)% of 3500 + 6(2/3) % of 6000 = ? + 552.5
What value should come in the place of (?) in the following questions.
336 ÷ 6 ÷ √16 * ? = 1400 ÷ 4
What will come in the place of question mark (?) in the given expression?
(18 × 8 + 24) × 4 = ?
Simplify the following expression:
(400 +175) ² - (400 – 175) ² / (400 × 175)
√(24²+285-8²-172) = ?²
26 X √25 + 15 - 80% of 120 = ?2
? = (22% of 25% of 60% of 3000) + 21
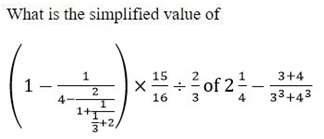
√? = 120 - 102 + ∛125



