Question
A Bullet is cylindrical up to a height of 40 cm and
conical above it. If its diameter is 35 cm and the slant height of the Conical part is 22cm, then the curved area of the bullet isSolution
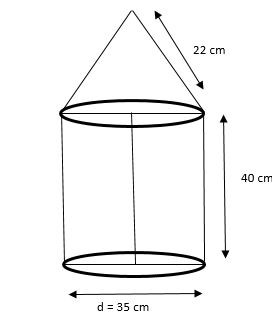Radius of Cone = 35/2 cm Curved Surface area of Conical Part of a bullet = πrl = 22/7×35/2 × 22 = 1210 cm² Curved Surface area of the Cylinder = 2πrh = 2 × 22/7×35/2 × 40 = 4400 cm² Total Surface area of a Bullet = 4400 + 1210 = 5610 cm²
The apex bank of India Reserve Bank of India (RBI) has announced that it has extended the deadline for periodic KYC updates by ?
What is the focus of ALTÉRRA, the investment fund announced by the UAE during COP-28?
Around _______ households sought work under the flagship Mahatma Gandhi National Rural Employment Guarantee Scheme (MGNREGS) in May, which is the highes...
 _____ became the winner of the Indian Pharma Leader of the year award?
What is the primary objective of the NPS Vatsalya scheme launched by the Finance Minister?
Which state government has planned to spend over Rs 180 crore during the 2023-24 financial year under the Mukhyamantri Laghu Udyog Protsahan Yojana (C...
Which of the following has won the L'Oeil d'Or 2022 at the Cannes Film Festival?
The critically endangered Asian giant tortoise was reintroduced into which protected area and district in Nagaland?
Which of the following was a major discovery made in the Sepahijala Wildlife Sanctuary in Tripura?
Which of the following statements regarding China-Pakistan Economic Corridor (CPEC) is not correct?
Relevant for Exams:
