Question
A cylinder of radius 7 cm is surmounted completely by a cone of same radius. Height of cylinder is 6
A cylinder of radius 7 cm is surmounted completely by a cone of same radius. Height of cylinder is 6
cm. Find the height of cone if volume of entire shape 1078 cubic
cm.
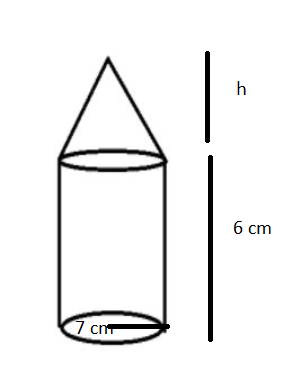Volume of cylinder = πr2h Volume of cylinder = 1/3 × πr2h Total volume given = 1078 => πr2h + 1/3 × πr2h = 1078 => 22/7 × 49 × (6 + 1/3 × h) = 1078 => (6 + 1/3 × h) = 1078/154 => h = 3More Mensuration Questions
- A rectangular piece of land has a perimeter of 66 metres and length of 18 metres. If the area of the land is to be divided into 9 equal portions, then what...
- If (x² + 1/x2) = 4, which of the options below is a possible value of x² - 1/x2 ?
- Compute the diameter of the incircle of a triangle where the semi-perimeter is 30 cm and the area is 90 cm².
- Calculate the area of a circular field whose circumference is equal to the perimeter of a rectangular field with a length of 60 m and a breadth of 45 m. (U...
- The sum of the radius and height of a cylinder is 34m. The total surface area of the cylinder is 5984 m². What is the volume (in m³) of the cylin...
- Find the length of the side of a regular octagon which is formed by cutting the corner of square of side 30 cm?
- A maximum-size sphere is cut from a hemisphere of radius r. Find the ratio of the volume of the sphere to the hemisphere. Radius of Hemispher
- Raman gave a certain amount to his son Ritesh for buying some pens and pencils. With this amount Ritesh can purchase either 10 pens or 30 pencils. Ri...
- The perimeter of 4 squares is 20 cm, 36 cm, 40 cm and 48 cm respectively. What will be the area of the square having perimeter equal to sum of edges of 4 s...
- In measuring the sides of a rectangle, there is an excess of 12% on one side and 10% deficit on the other. Then the error percent in the area is
Hey! Ask a query
Please enter email id
The email must be a valid email address.
Please enter Mobile Number
Please enter valid Mobile Number
Please enter your Doubt
