Question
A tree stands tall with a height of 54 meters. From a
point 'x' meters away from its base, the angle of elevation to the top of the tree is 60°. Determine the value of 'x'.Solution
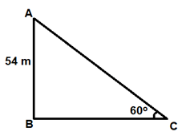In the given figure, let points 'A' and 'B' represent the top of the tree and the base of the tree, respectively and let 'C' represents the point on the ground that is 'x' metres away from the base of the tree (BC = x).In right triangle ABCtan 60o = (AB/x)Or, (54/x) = √3So, x = 54 ÷ √3 = 18√3 metres
Pipe ‘A’ can fill a tank in 20 hours while pipe ‘B’ takes 30 hours to empty it. Pipe ‘A’ is opened alone when the tank was empty and after 1...
Tap A can fill a tank in 8 hours. Tap B can fill 12.5% part of the same tank in 2 hours, whereas Tap C can alone empty a tank in ‘x’ hours. 5/8 part...
Two pipes A and B can fill a tank in 24 min., and 32 min, respectively. If both the pipes are opened simultaneously, after how much time B should be clo...
- Pipe X can fill a pool in 18 hours and pipe Y in 36 hours. If both the pipes are opened in an empty pool, how much time will they take to fill it?
Two pipes, A and B, can independently fill the tank in 20 minutes and 25 minutes respectively, while pipe C can empty 7 gallons from the tank in 5 minut...
Pipe A fills a tank in 60 minutes, and pipe B can do it in 90 minutes. There’s also a pipe C that drains the tank in 180 minutes. If all three pipes a...
Pipe 'A' takes 20 minutes to fill half of the tank. Pipe 'B' is twice as efficient as pipe 'A'. Find the percentage of the tank filled by both in 8 minu...
Two pipes 'P' and 'Q' together can fill a tank in 16 minutes while 'Q' alone can fill the tank in 24 minutes. How much time does pipe 'P' alone need to ...
Pipe ‘A’ can fill a tank in 30 hours whereas leak ‘A’ can empty it in 45 hours. If they both operate along with pipe ‘B’, then the given tan...
- Pipe 'A' can fill a tank in 20 hours. Pipe 'B' is ____% as efficient as pipe 'A'. If both pipes are opened simultaneously, the tank will be completely full...
