Question
The area of a rhombus is 1,600 cm², and the lengths of its
diagonals are in the ratio 5:4. A circle is constructed with the smaller diagonal as the diameter. Find the difference between the area of the circle and 75% of the rhombus's area. (Take π = 3)Solution
ATQ,
Let diagonals = 5x and 4x
Area = (1/2) × 5x × 4x = 10x²
1600 = 10x² → x² = 160 → x = √160 ≈ 12.65
Smaller diagonal = 4x ≈ 50.6 cm
Radius ≈ 25.3 cm
Area of circle ≈ 3 × (25.3)² ≈ 3 × 640 ≈ 1920 cm²
75% of rhombus = 0.75 × 1600 = 1200 cm²
Difference ≈ 1920 - 1200 = 720 cm²
More Circle Questions
2(3/4) of 2880 + 54% of 7520 - ? = 302
Find the value of the following expression:
372 ÷ 56 × 7 – 5 + 2
- What will come in place of (?), in the given expression.
(5³ + 3²) × 2 = ? (1225/25) - (192/96) + (50/5) = ?
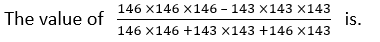
What will come in the place of question mark (?) in the given expression?
(555 + 385 - 535) ÷ 15 X ? = 36 X 30
- What will come in place of (?), in the given expression.
75% of 640 – 20% of 150 = ? `(21 xx 51 + 54)/(9 xx 14 - 30 )` =?
95% of 830 - ? % of 2770 = 650
Relevant for Exams:
