Question
In the given diagram, point 'O' represents the center of
a circle, while AB and DE are two distinct chords within the circle. The line segment OC is perpendicular to the chord AB, and the segment OF is perpendicular to the chord DE. The length of chord AB is provided as 24 cm, and the distance CF from the center to the perpendicular intersection with chord DE is (5 + 4√5) cm. The radius of the circle measures 13 cm. Determine the length of chord DE.Solution
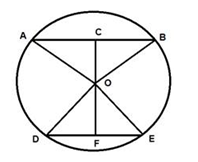The perpendicular from the centre of the circle to its chord, bisects the chord. So, AC = CB = (24/2) = 12 cm Similarly, DF = FE In right rAOC, using Pythagoras theorem, AO2 = AC2 + CO2 Or, 132 = 122 + CO2 So, CO2 = 169 - 144 = 25 Or, CO = √25 = 5 cm And, OF = CF - CO = 5 + 4√5 - 5 = 4√5 cm In right rDOF, using Pythagoras theorem, DO2 = DF2 + OF2 So, DF2 = 132 - (4√5)2 Or, DF2 = 169 - 80 = 89 So, DF = √89 cm DE = DF + FE = 2DF = 2√89 cmÂ
Which of the following sports personality recently awarded the prestigious Padma Bhushan?
Which organization initiated Project REPLAN (Reducing Plastic from Nature)?Â
The Junagarh inscription of Rudradaman is written in which language?
Between which two rivers was the ancient city of Takshashila located?
Identify the mineral critical for high-tech applications like batteries:
The thirty-first meeting of the Monetary Policy Committee (MPC), constituted under section 45ZB of the Reserve Bank of India Act, 1934, will be held from?
Who is considered the hero in Kalidasa's Malvikagnimitram, referred to as "Raja"?
Which state recently launched Nanaji Deshmukh Krishi Sanjivani Yojna to promote climate resilient agriculture?
Which type of rock is granite classified as?
Who among the following became the first woman Chairperson of Indian Banks' Association (IBA)?
