Question
Average of five two-digit consecutive even natural
numbers is (m + 9), and the average of five two-digit consecutive odd natural numbers is (n - 6). When each set is arranged in increasing order, sum of the fourth even number and the second odd number is 59. The fifth odd number is three less than the second even number. Which of the following statement(s) is/are true? I. The difference between the fourth even number and the first odd number is 15. II. The third odd number is a perfect square. III. The first even number is greater than 27.Solution
Five even numbers: a, (a + 2) , (a + 4) , (a + 6) , (a + 8) Five odd numbers: b, (b + 2) , (b + 4) , (b + 6) , (b + 8) Given, (a + 6) + (b + 2) = 59 Or, a + b = 51 ------ (I) b + 8 = a + 2 - 3 Or, a – b = 9 --------- (II) On adding equation I and II, We get, a + b + a – b = 51 + 9 Or, 2a = 60 Or, 'a' = 30 On putting value of 'a' in equation II, We get, 'b' = 30 - 9 = 21 So, the five even numbers: 30, 32, 34, 36, 38
And the five odd numbers: 21, 23, 25, 27, 29
Statement I:
Required difference = 36 - 21 = 15
So, statement I is true.
Statement II:
Third odd number = 25, which is a perfect square.
So, statement II is true.
Statement III:
First even number = 30, and 30 > 27.
So, statement III is true.
Therefore, all three statements I, II and III are true.
If a + b + c = 9 and ab + bc + ca = 20, then find the value of a² + b² + c².
- 8p 3 - 27q 3 - 36p 2 q + 54pq 2 is equivalent to:
If, ( a + b = 12 ) and ( a² + b² = 80 ), then find the value of (a³ + b³).
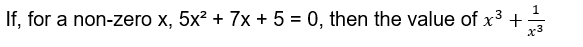
- If (510 – 486 + 240) ÷ 8 + √2500 = x, then {(x/2) + 18} = ?
(u - 5) 2 + (v + 2) 2 + (w – 4) 2 = 0, then find the value of 4u - v + w.
Given that x = 80, y = -35 and z = -45, Determine the value of [(x³ + y³ + z³)/10³]
If (x –4)3+(x–5)3+(x–6)3 = 3(x–4)(x–5)(x–6), Then x = ?
When positive numbers x, y and z are divided by 31, the remainders are 17, 24 and 27, respectively. When (4x - 2y + 3z) is divided by 31, the remainder ...
If x² + x = 11
find (x+4)³ +1/((x+4)³)



