Question
In the context of the Central Limit Theorem (CLT), which
of the following statements is correct?Solution
The Central Limit Theorem (CLT) is one of the foundational principles of statistics. It states that regardless of the shape of the population distribution (whether skewed, bimodal, or uniform), the sampling distribution of the sample mean will approach a normal distribution as the sample size increases. This phenomenon holds true even if the original population distribution is not normal. However, the convergence to normality improves with larger sample sizes, typically when n≥30n \ geq 30 n≥30, which is often cited as a rule of thumb. For example, consider a population with a skewed distribution, such as household incomes. Individual samples drawn from this population might reflect its skewed nature. However, if you repeatedly take samples and compute their means, plotting these sample means will produce a distribution that becomes increasingly normal as the number of samples grows. This property allows statisticians to apply inferential methods, such as hypothesis testing and confidence intervals, based on the assumption of normality. Why Other Options Are Wrong:
- A. The CLT states that the distribution of a sample becomes skewed as the sample size increases:
- This is incorrect because the CLT describes how the sampling distribution of the sample mean becomes normal as the sample size increases, not skewed. In fact, larger sample sizes help mitigate the effects of skewness in the population distribution when examining the sampling distribution of the mean.
- B. The CLT applies only when the population distribution is normal:
- D. The CLT ensures that the population mean and sample mean are always identical:
- E. The CLT applies to small sample sizes, even if the population distribution is heavily skewed:
- Rs. 36000 is shared among 'Pawan', 'Qureshi' and 'Raju' such that 'Pawan' receives (3/5) of what 'Qureshi' gets and (3/2) times of what 'Raju' gets. What i...
- Mixture X has milk and water in the ratio 5:3, while mixture Y has them in the ratio 4:5. 64 litres of X and 45 litres of Y are combined. What is the ratio...
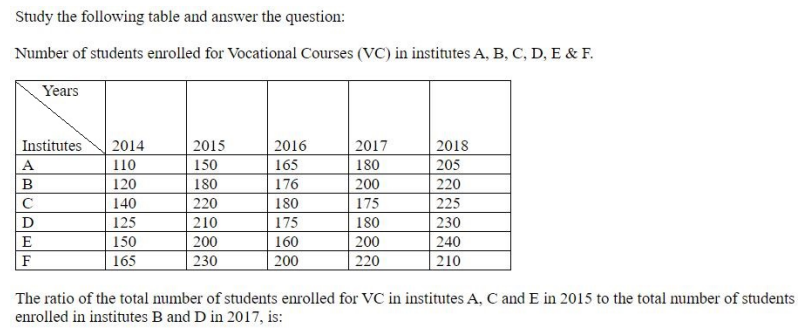
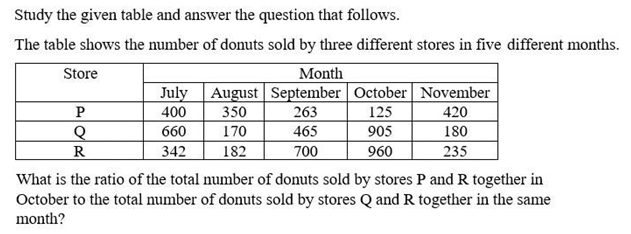
A box contains red, blue, and green balls in the ratio of 3:4:5. If there are 60 balls in total, how many blue balls are there?
In a showroom, 65% of the vehicles are two-wheelers and the remaining are four-wheelers. Find the ratio of the number of wheels of two-wheelers to that ...
120 is divided into two parts in such a way that the sixth part of the first part and the seventh part of the second are in the ratio 5 : 6. How much pe...
If A: B = 2:3 and B: C = 3:4 find the value of (A+B): (B+C): (C+A).
The sides of a right-angled triangle are in the ratio 12:13:5. If the total perimeter of the triangle is 120 cm, determine its area.
In an alloy of three metals, ratio of the quantity of gold, silver and platinum is 5:6:8, respectively. If total quantity of silver and platinum togethe...
Relevant for Exams:



