Question

    The angle of elevation of a tower from a certain point

    of bus stand is 30°. When a man walks 5m ahead in the direction of the tower, the angle of elevation becomes 60°. What is the height of the tower?
    A (3√3)/2 m Correct Answer Incorrect Answer
    B 2√3 m Correct Answer Incorrect Answer
    C (5√3)/2 m Correct Answer Incorrect Answer
    D 3√3 m Correct Answer Incorrect Answer

    Solution

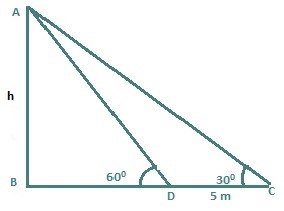    Let, the height of the post = AB = ‘h’ m From ΔACB, ∠ACB = 30° [∵ given] tan ∠ACB = perpendicular/base ⇒ tan 30° = AB/BC ⇒ 1/√3 = h/BC ⇒ BC = h√3 ... (1) From ΔADB, ∠ADB = 60° [∵ given] tan ∠ADB = perpendicular/base ⇒ tan 60° = AB/BD ⇒ √3 = h/BD ⇒ BD = h/√3 ... (2) According to the question: BC - BD = 5 ⇒ h√3 - h/√3 = 5 ⇒ 2h/√3 = 5 ⇒ h = (5√3)/2 m

    Practice Next
    More Difficult level Section Tests Questions

    Relevant for Exams:

    ask-question